
SL Paper 3
A radio wave of wavelength is incident on a conductor. The graph shows the variation with wavelength of the maximum distance d travelled inside the conductor.
For = 5.0 x 105 m, calculate the
The graph shows the variation with wavelength of d 2. Error bars are not shown and the line of best-fit has been drawn.
A student states that the equation of the line of best-fit is d 2 = a + b. When d 2 and are expressed in terms of fundamental SI units, the student finds that a = 0.040 x 10–4 and b = 1.8 x 10–11.
Suggest why it is unlikely that the relation between d and is linear.
fractional uncertainty in d.
percentage uncertainty in d 2.
State the fundamental SI unit of the constant a and of the constant b.
Determine the distance travelled inside the conductor by very high frequency electromagnetic waves.
Markscheme
it is not possible to draw a straight line through all the error bars
OR
the line of best-fit is curved/not a straight line
Treat as neutral any reference to the origin.
Allow “linear” for “straight line”.
[1 mark]
d = 0.35 ± 0.01 AND Δd = 0.05 ± 0.01 «cm»
«» = 0.14
OR
or 14% or 0.1
Allow final answers in the range of 0.11 to 0.18.
Allow [1 max] for 0.03 to 0.04 if = 5 × 106 m is used.
[2 marks]
28 to 30%
Allow ECF from (b)(i), but only accept answer as a %
[1 mark]
a: m2
b: m
Allow answers in words
[2 marks]
ALTERNATIVE 1 – if graph on page 4 is used
d 2 = 0.040 x 10–4 «m2»
d = 0.20 x 10–2 «m»
ALTERNATIVE 2 – if graph on page 2 is used
any evidence that d intercept has been determined
d = 0.20 ± 0.05 «cm»
For MP1 accept answers in range of 0.020 to 0.060 «cm2» if they fail to use given value of “a”.
For MP2 accept answers in range 0.14 to 0.25 «cm» .
[2 marks]
Examiners report
The equipment shown in the diagram was used by a student to investigate the variation with volume, of the pressure p of air, at constant temperature. The air was trapped in a tube of constant cross-sectional area above a column of oil.
The pump forces oil to move up the tube decreasing the volume of the trapped air.
The student measured the height H of the air column and the corresponding air pressure p. After each reduction in the volume the student waited for some time before measuring the pressure. Outline why this was necessary.
The following graph of p versus was obtained. Error bars were negligibly small.
The equation of the line of best fit is .
Determine the value of b including an appropriate unit.
Outline how the results of this experiment are consistent with the ideal gas law at constant temperature.
The cross-sectional area of the tube is 1.3 × 10–3m2 and the temperature of air is 300 K. Estimate the number of moles of air in the tube.
The equation in (b) may be used to predict the pressure of the air at extremely large values of . Suggest why this will be an unreliable estimate of the pressure.
Markscheme
in order to keep the temperature constant
in order to allow the system to reach thermal equilibrium with the surroundings/OWTTE
Accept answers in terms of pressure or volume changes only if clearly related to reaching thermal equilibrium with the surroundings.
[1 mark]
recognizes b as gradient
calculates b in range 4.7 × 104 to 5.3 × 104
Pam
Award [2 max] if POT error in b.
Allow any correct SI unit, eg kgs–2.
[3 marks]
thus ideal gas law gives
so graph should be «a straight line through origin,» as observed
[2 marks]
OR correct substitution of one point from the graph
Answer must be to 1 or 2 SF.
Allow ECF from (b).
[2 marks]
very large means very small volumes / very high pressures
at very small volumes the ideal gas does not apply
OR
at very small volumes some of the assumptions of the kinetic theory of gases do not hold
[2 marks]
Examiners report
An apparatus is used to verify a gas law. The glass jar contains a fixed volume of air. Measurements can be taken using the thermometer and the pressure gauge.
The apparatus is cooled in a freezer and then placed in a water bath so that the temperature of the gas increases slowly. The pressure and temperature of the gas are recorded.
The graph shows the data recorded.
Identify the fundamental SI unit for the gradient of the pressure–temperature graph.
The experiment is repeated using a different gas in the glass jar. The pressure for both experiments is low and both gases can be considered to be ideal.
(i) Using the axes provided in (a), draw the expected graph for this second experiment.
(ii) Explain the shape and intercept of the graph you drew in (b)(i).
Markscheme
kg m–1 s–2 K–1
i
any straight line that either goes or would go, if extended, through the origin
ii
for ideal gas p is proportional to T / P= nRT/V
gradient is constant /graph is a straight line
line passes through origin / 0,0
Examiners report
In a simple pendulum experiment, a student measures the period T of the pendulum many times and obtains an average value T = (2.540 ± 0.005) s. The length L of the pendulum is measured to be L = (1.60 ± 0.01) m.
Calculate, using , the value of the acceleration of free fall, including its uncertainty. State the value of the uncertainty to one significant figure.
In a different experiment a student investigates the dependence of the period T of a simple pendulum on the amplitude of oscillations θ. The graph shows the variation of with θ, where T0 is the period for small amplitude oscillations.
The period may be considered to be independent of the amplitude θ as long as . Determine the maximum value of θ for which the period is independent of the amplitude.
Markscheme
«» 0.0997
OR
1.0%
hence g = (9.8 ± 0.1) «ms−2» OR Δg = 0.1 «ms−2»
For the first marking point answer must be given to at least 2 dp.
Accept calculations based on
[3 marks]
θmax = 22 «º»
Accept answer from interval 20 to 24.
[2 marks]
Examiners report
The circuit shown may be used to measure the internal resistance of a cell.
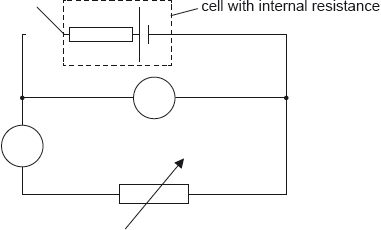
The ammeter used in the experiment in (b) is an analogue meter. The student takes measurements without checking for a “zero error” on the ammeter.
An ammeter and a voltmeter are connected in the circuit. Label the ammeter with the letter A and the voltmeter with the letter V.
In one experiment a student obtains the following graph showing the variation with current I of the potential difference V across the cell.
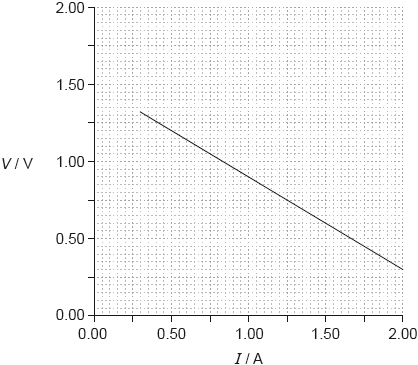
Using the graph, determine the best estimate of the internal resistance of the cell.
State what is meant by a zero error.
After taking measurements the student observes that the ammeter has a positive zero error. Explain what effect, if any, this zero error will have on the calculated value of the internal resistance in (b).
Markscheme
correct labelling of both instruments
[1 mark]
V = E – Ir
large triangle to find gradient and correct read-offs from the line
OR
use of intercept E = 1.5 V and another correct data point
internal resistance = 0.60 Ω
For MP1 – do not award if only is used.
For MP2 points at least 1A apart must be used.
For MP3 accept final answers in the range of 0.55 Ω to 0.65 Ω.
[3 marks]
a non-zero reading when a zero reading is expected/no current is flowing
OR
a calibration error
OWTTE
Do not accept just “systematic error”.
[1 mark]
the error causes «all» measurements to be high/different/incorrect
effect on calculations/gradient will cancel out
OR
effect is that value for r is unchanged
Award [1 max] for statement of “no effect” without valid argument.
OWTTE
[2 marks]
Examiners report
A student studies the relationship between the centripetal force applied to an object undergoing circular motion and its period .
The object (mass ) is attached by a light inextensible string, through a tube, to a weight which hangs vertically. The string is free to move through the tube. A student swings the mass in a horizontal, circular path, adjusting the period of the motion until the radius is constant. The radius of the circle and the mass of the object are measured and remain constant for the entire experiment.
© International Baccalaureate Organization 2020.
The student collects the measurements of five times, for weight . The weight is then doubled () and the data collection repeated. Then it is repeated with and . The results are expected to support the relationship
In reality, there is friction in the system, so in this case is less than the total centripetal force in the system. A suitable graph is plotted to determine the value of experimentally. The value of was also calculated directly from the measured values of and .
State why the experiment is repeated with different values of .
Predict from the equation whether the value of found experimentally will be larger, the same or smaller than the value of calculated directly.
The measurements of were collected five times. Explain how repeated measurements of reduced the random error in the final experimental value of .
Outline why repeated measurements of would not reduce any systematic error in .
Markscheme
In order to draw a graph « of versus »
OR
to confirm proportionality between « and »
OR
to confirm relationship between « and »
OR
because W is the independent variable in the experiment ✓
OWTTE
ALTERNATIVE 1
OR
centripetal force is larger «than » / is smaller «than centripetal» ✓
«so» experimental is smaller «than calculated value» ✓
ALTERNATIVE 2 (refers to graph)
reference to «friction force is» a systematic error «and does not affect gradient» ✓
«so» is the same ✓
MP2 awarded only with correct justification.
Candidates can gain zero, MP1 alone or full marks.
OWTTE
mention of mean/average value «of » ✓
this reduces uncertainty in / result
OR
more accurate/precise ✓
Reference to “random errors average out” scores MP1
Accept “closer to true value”, “more reliable value” OWTTE for MP2
systematic errors «usually» constant/always present/ not influenced by repetition ✓
OWTTE
Examiners report
Most candidates scored. Different wording was used to express the aim of confirming the relationship.
Most successful candidates chose to consider a single point then concluding that the calculated mr would be smaller than the real value as W < centripetal force, or even went into analysing the dependence of the frictional force with W. Many were able to deduce this. Some candidates thought that a graph would still have the same gradient (if friction was constant) and mentioned systematic error, so mr was not changed which was also accepted.
Most candidates stated that the mean of 5 values of T was used to obtain an answer closer to the true value if there were no systematic errors. Some just repeated the question.
Usually very well answered acknowledging that systematic errors are constant and present throughout all measurements.
A student carries out an experiment to determine the variation of intensity of the light with distance from a point light source. The light source is at the centre of a transparent spherical cover of radius C. The student measures the distance x from the surface of the cover to a sensor that measures the intensity I of the light.
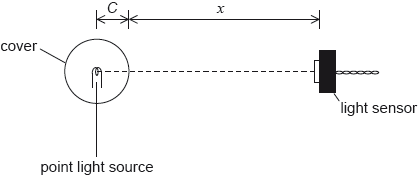
The light source emits radiation with a constant power P and all of this radiation is transmitted through the cover. The relationship between I and x is given by
The student obtains a set of data and uses this to plot a graph of the variation of with x.
This relationship can also be written as follows.
Show that .
Estimate C.
Determine P, to the correct number of significant figures including its unit.
Explain the disadvantage that a graph of I versus has for the analysis in (b)(i) and (b)(ii).
Markscheme
combines the two equations to obtain result
«for example = K2(C + x)2 = (C + x)2»
OR
reverse engineered solution – substitute K = into = K2(C + x)2 to get I =
There are many ways to answer the question, look for a combination of two equations to obtain the third one
[1 mark]
extrapolating line to cross x-axis / use of x-intercept
OR
Use C =
OR
use of gradient and one point, correctly substituted in one of the formulae
accept answers between 3.0 and 4.5 «cm»
Award [1 max] for negative answers
[2 marks]
ALTERNATIVE 1
Evidence of finding gradient using two points on the line at least 10 cm apart
Gradient found in range: 115–135 or 1.15–1.35
Using P = to get value between 6.9 × 10–4 and 9.5 × 10–4 «W» and POT correct
Correct unit, W and answer to 1, 2 or 3 significant figures
ALTERNATIVE 2
Finds from use of one point (x and y) on the line with x > 6 cm and C from(b)(i)to use in I = or = Kx + KC
Correct re-arrangementto get P between 6.9 × 10–4 and 9.5 × 10–4 «W» and POT correct
Correct unit, W and answer to 1, 2 or 3 significant figures
Award [3 max] for an answer between 6.9 W and 9.5 W (POT penalized in 3rd marking point)
Alternative 2 is worth [3 max]
[4 marks]
this graph will be a curve / not be a straight line
more difficult to determine value of K
OR
more difficult to determine value of C
OR
suitable mathematical argument
OWTTE
[2 marks]
Examiners report
In an experiment to measure the specific latent heat of vaporization of water Lv, a student uses an electric heater to boil water. A mass m of water vaporizes during time t. Lv may be calculated using the relation
where V is the voltage applied to the heater and I the current through it.
Outline why, during the experiment, V and I should be kept constant.
Outline whether the value of Lv calculated in this experiment is expected to be larger or smaller than the actual value.
A student suggests that to get a more accurate value of Lv the experiment should be performed twice using different heating rates. With voltage and current V1, I1 the mass of water that vaporized in time t is m1. With voltage and current V2, I2 the mass of water that vaporized in time t is m2. The student now uses the expression
to calculate Lv. Suggest, by reference to heat losses, why this is an improvement.
Markscheme
to provide a constant heating rate / power
OR
to have m proportional to t ✔
due to heat losses «VIt is larger than heat into liquid» ✔
Lv calculated will be larger ✔
heat losses will be similar / the same for both experiments
OR
heat loss presents systematic error ✔
taking the difference cancels/eliminates the effect of these losses
OR
use a graph to eliminate the effect ✔
Examiners report
An experiment to find the internal resistance of a cell of known emf is to be set. The following equipment is available:
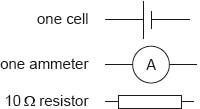
Draw a suitable circuit diagram that would enable the internal resistance to be determined.
It is noticed that the resistor gets warmer. Explain how this would affect the calculated value of the internal resistance.
Outline how using a variable resistance could improve the accuracy of the value found for the internal resistance.
Markscheme
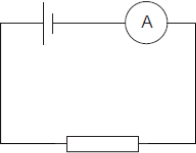
ammeter and resistor in series
[1 mark]
resistance of resistor would increase / be greater than 10 Ω
R + r «from ε = I(R + r)» would be overestimated / lower current
therefore calculated r would be larger than real
Award MP3 only if at least one previous mark has been awarded.
[3 marks]
variable resistor would allow for multiple readings to be made
gradient of V-I graph could be found «to give r»
Award [1 max] for taking average of multiple.
[2 marks]
Examiners report
A magnetized needle is oscillating on a string about a vertical axis in a horizontal magneticfield B. The time for 10 oscillations is recorded for different values of B.
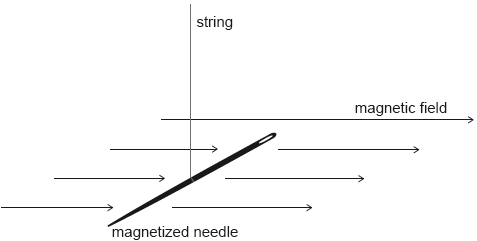
The graph shows the variation with B of the time for 10 oscillations together with the uncertainties in the time measurements. The uncertainty in B is negligible.
Draw on the graph the line of best fit for the data.
Write down the time taken for one oscillation when B = 0.005 T with its absolute uncertainty.
A student forms a hypothesis that the period of one oscillation P is given by:
where K is a constant.
Determine the value of K using the point for which B = 0.005 T.
State the uncertainty in K to an appropriate number of significant figures.
State the unit of K.
The student plots a graph to show how P2 varies with for the data.
Sketch the shape of the expected line of best fit on the axes below assuming that the relationship is verified. You do not have to put numbers on the axes.
State how the value of K can be obtained from the graph.
Markscheme
smooth line, not kinked, passing through all the error bars.
[1 mark]
0.84 ± 0.03 «s»
Accept any value from the range: 0.81 to 0.87.
Accept uncertainty 0.03 OR 0.025.
[1 mark]
«»
«K =(0.059 ± 0.002)»
uncertainty given to 1sf
Allow ECF [3 max] if 10T is used.
Award [3] for BCA.
[3 marks]
Accept or in words.
[1 mark]
straight AND ascending line
through origin
[2 marks]
[1 mark]
Examiners report
The resistance R of a wire of length L can be measured using the circuit shown.
In one experiment the wire has a uniform diameter of d = 0.500 mm. The graph shows data obtained for the variation of R with L.
The gradient of the line of best fit is 6.30 Ω m–1.
Estimate the resistivity of the material of the wire. Give your answer to an appropriate number of significant figures.
Explain, by reference to the power dissipated in the wire, the advantage of the fixed resistor connected in series with the wire for the measurement of R.
The experiment is repeated using a wire made of the same material but of a larger diameter than the wire in part (a). On the axes in part (a), draw the graph for this second experiment.
Markscheme
evidence of use of ρ = given gradient × wire area
OR
substitution of values from a single data point with wire area ✔
✔
NOTE: Check POT is correct.
MP2 must be correct to exactly 3 s.f.
measurement should be performed at a constant temperature
OR
resistance of wire changes with temperature ✔
series resistance prevents the wire from overheating
OR
reduces power dissipated in the wire ✔
by reducing voltage across/current through the wire ✔
ANY straight line going through the origin if extrapolated ✔
ANY straight line below existing line with smaller gradient ✔
Examiners report
In an investigation to measure the acceleration of free fall a rod is suspended horizontally by two vertical strings of equal length. The strings are a distance d apart.
When the rod is displaced by a small angle and then released, simple harmonic oscillations take place in a horizontal plane.
The theoretical prediction for the period of oscillation T is given by the following equation
where c is a known numerical constant.
In one experiment d was varied. The graph shows the plotted values of T against . Error bars are negligibly small.
State the unit of c.
A student records the time for 20 oscillations of the rod. Explain how this procedure leads to a more precise measurement of the time for one oscillation T.
Draw the line of best fit for these data.
Suggest whether the data are consistent with the theoretical prediction.
The numerical value of the constant c in SI units is 1.67. Determine g, using the graph.
Markscheme
✔
Accept other power of tens multiples of , eg: .
measured uncertainties «for one oscillation and for 20 oscillations» are the same/similar/OWTTE
OR
% uncertainty is less for 20 oscillations than for one ✔
dividing «by 20» / finding mean reduces the random error ✔
Straight line touching at least 3 points drawn across the range ✔
It is not required to extend the line to pass through the origin.
theory predicts proportional relation «, slope = Td = = constant » ✔
the graph is «straight» line through the origin ✔
correctly determines gradient using points where ΔT≥1.5s
OR
correctly selects a single data point with T≥1.5s ✔
manipulation with formula, any new and correct expression to enable g to be determined ✔
Calculation of g ✔
With g in range 8.6 and 10.7 «m s−2» ✔
Allow range 0.51 to 0.57.
Examiners report
A student investigates how the period T of a simple pendulum varies with the maximum speed v of the pendulum’s bob by releasing the pendulum from rest from different initial angles. A graph of the variation of T with v is plotted.
Suggest, by reference to the graph, why it is unlikely that the relationship between T and v is linear.
Determine the fractional uncertainty in v when T = 2.115 s, correct to one significant figure.
The student hypothesizes that the relationship between T and v is T = a + bv2, where a and b are constants. To verify this hypothesis a graph showing the variation of T with v2 is plotted. The graph shows the data and the line of best fit.
Determine b, giving an appropriate unit for b.
The lines of the minimum and maximum gradient are shown.
Estimate the absolute uncertainty in a.
Markscheme
a straight line cannot be drawn through all error bars
OR
the graph/line of best fit is /curved/not straight/parabolic etc.
OR
graph has increasing/variable gradient ✔
NOTE: Do not allow “a line cannot be drawn through all error bars” without specifying “straight”.
AND ✔
«»0.04 ✔
NOTE: Accept 4 %
use of 2 correct points on the line with Δv2 > 2 ✔
b in range 0.012 to 0.013 ✔
s3 m–2 ✔
«s» ±0.001 «s» AND «s» ±0.001 «s» ✔
«» 0.003 «s» ✔
Examiners report
In an experiment to measure the acceleration of free fall a student ties two different blocks of masses m1 and m2 to the ends of a string that passes over a frictionless pulley.
The student calculates the acceleration a of the blocks by measuring the time taken by the heavier mass to fall through a given distance. Their theory predicts that and this can be re-arranged to give .
In a particular experiment the student calculates that a = (0.204 ±0.002) ms–2 using m1 = (0.125 ±0.001) kg and m2 = (0.120 ±0.001) kg.
Calculate the percentage error in the measured value of g.
Deduce the value of g and its absolute uncertainty for this experiment.
There is an advantage and a disadvantage in using two masses that are almost equal.
State and explain the advantage with reference to the magnitude of the acceleration that is obtained.
There is an advantage and a disadvantage in using two masses that are almost equal.
State and explain the disadvantage with reference to your answer to (a)(ii).
Markscheme
error in m1 + m2 is 1 % OR error in m1 − m2 is 40 % OR error in a is 1 % ✔
adds percentage errors ✔
so error in g is 42 % OR 40 % OR 41.8 % ✔
Allow answer 0.42 or 0.4 or 0.418.
Award [0] for comparing the average value with a known value, e.g. 9.81 m s-2.
g = 9.996 «m s−2» OR Δg = 4.20 «m s−2» ✔
g = (10 ± 4) «m s−2»
OR
g = (10.0 ± 4.2) «m s−2» ✔
Award [1] max for not proper significant digits or decimals use, such as: 9.996±4.178 or 10±4.2 or 10.0±4 or 10.0±4.18« m s−2 » .
the acceleration would be small/the time of fall would be large ✔
easier to measure /a longer time of fall reduces the % error in the time of fall and «hence acceleration» ✔
Do not accept ideas related to the mass/moment of inertia of the pulley.
the percentage error in the difference of the masses is large ✔
leading to a large percentage error/uncertainty in g/of the experiment ✔
Do not accept ideas related to the mass/moment of inertia of the pulley.
Examiners report
Atwoods machine a) is a quite straightforward question that tests the ability to propagate uncertainties through calculations. Almost all candidates proved the ability to add percentages or relative calculations, however, many weaker candidates failed in the percentage uncertainty when subtracting the two masses.
Many average candidates did not use the correct number of significant figures and wrote the answers inappropriately. Only the best candidates rounded out and wrote the proper answer of 10±4 ms−2. Some candidates did not propagate uncertainties and only compared the average calculated value with the known value 9.81 ms−2.
Q 1 b) was quite well answered. Only the weakest candidates presented difficulty in understanding simple mechanics.
In part ii) many were able to appreciate that the resultant percentage error in “g” was relatively large however linking this with what caused the large uncertainty (that is, the high % error from the small difference in masses) proved more challenging.
A student measures the refractive index of water by shining a light ray into a transparent container.
IO shows the direction of the normal at the point where the light is incident on the container. IX shows the direction of the light ray when the container is empty. IY shows the direction of the deviated light ray when the container is filled with water.
The angle of incidence θ is varied and the student determines the position of O, X and Y for each angle of incidence.
The table shows the data collected by the student. The uncertainty in each measurement of length is ±0.1 cm.
(i) Outline why OY has a greater percentage uncertainty than OX for each pair of data points.
(ii) The refractive index of the water is given by when OX is small.
Calculate the fractional uncertainty in the value of the refractive index of water for OX = 1.8 cm.
A graph of the variation of OY with OX is plotted.
(i) Draw, on the graph, the error bars for OY when OX = 1.8 cm and when OY = 5.8 cm.
(ii) Determine, using the graph, the refractive index of the water in the container for values of OX less than 6.0 cm.
(iii) The refractive index for a material is also given by where i is the angle of incidence and r is the angle of refraction.
Outline why the graph deviates from a straight line for large values of OX.
Markscheme
i
OY always smaller than OX AND uncertainties are the same/0.1
« so fraction »
ii
AND
= 0.13 OR 13%
Watch for correct answer even if calculation continues to the absolute uncertainty.
i
total length of bar = 0.2 cm
Accept correct error bar in one of the points: OX= 1.8 cm OR OY= 5.8 cm (which is not a measured point but is a point on the interpolated line) OR OX= 5.8 cm.
Ignore error bar of OX.
Allow range from 0.2 to 0.3 cm, by eye.
ii
suitable line drawn extending at least up to 6 cm
OR
gradient calculated using two out of the first three data points
inverse of slope used
value between 1.30 and 1.60
If using one value of OX and OY from the graph for any of the first three data points award [2 max].
Award [3] for correct value for each of the three data points and average.
If gradient used, award [1 max].
iii
«the equation n=» involves a tan approximation/is true only for small θ «when sinθ = tanθ»
OR
«the equation n=» uses OI instead of the hypotenuse of the ∆IOX or IOY
OWTTE
Examiners report
A spherical soap bubble is made of a thin film of soapy water. The bubble has an internal air pressure and is formed in air of constant pressure . The theoretical prediction for the variation of is given by the equation
where is a constant for the thin film and is the radius of the bubble.
Data for and were collected under controlled conditions and plotted as a graph showing the variation of with .
Suggest whether the data are consistent with the theoretical prediction.
Show that the value of is about 0.03.
Identify the fundamental units of .
In order to find the uncertainty for , a maximum gradient line would be drawn. On the graph, sketch the maximum gradient line for the data.
The percentage uncertainty for is . State , with its absolute uncertainty.
The expected value of is . Comment on your result.
Markscheme
«theory suggests» is proportional to ✓
graph/line of best fit is straight/linear «so yes»
OR
graph/line of best fit passes through the origin «so yes» ✓
MP1: Accept ‘linear’
MP2 do not award if there is any contradiction
eg: graph not proportional, does not pass through origin.
gradient «»
OR
use of equation with coordinates of a point ✓
✓
MP1 allow gradients in range to
MP2 allow a range to for
✓
Accept
straight line, gradient greater than line of best fit, and within the error bars ✓
« of » =
OR
« of » = ✓
rounds uncertainty to 1sf
OR
✓
Allow ECF from (b)(i)
Award [2] marks for a bald correct answer
Experimental value matches this/correct, as expected value within the range ✓
OR
experimental value does not match/incorrect, as it is not within range ✓
Examiners report
Many students obtained full marks here although a significant number did not acknowledge that the graph was through the origin and lost a mark.
Very well answered either by obtaining the gradient or replacing with the coordinates of a point.
Although the question was specifically about the fundamental units, several candidates lost the mark by answering Pa m.
Almost all candidates were able to draw the correct maximum gradient line.
Well answered. A significant number did not round the uncertainty to match the value of gamma.
To determine the acceleration due to gravity, a small metal sphere is dropped from rest and the time it takes to fall through a known distance and open a trapdoor is measured.
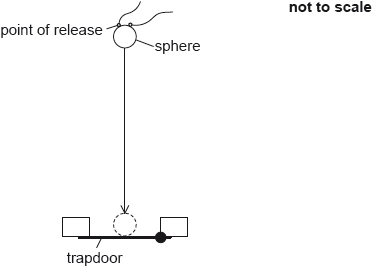
The following data are available.
Determine the distance fallen, in m, by the centre of mass of the sphere including an estimate of the absolute uncertainty in your answer.
Using the following equation
calculate, for these data, the acceleration due to gravity including an estimate of the absolute uncertainty in your answer.
Markscheme
distance fallen = 654 – 12 = 642 «mm»
absolute uncertainty = 2 + 0.1 «mm» ≈ 2 × 10–3 «m» or = 2.1 × 10–3 «m» or 2.0 × 10–3 «m»
Accept answers in mm or m
[2 marks]
«a = » = 9.744 «ms–2»
fractional uncertainty in distance = AND fractional uncertainty in time =
total fractional uncertainty = «= 0.00311 + 2 × 0.00551»
total absolute uncertainty = 0.1 or 0.14 AND same number of decimal places in value and uncertainty, ie: 9.7 ± 0.1 or 9.74 ± 0.14
Accept working in % for MP2 and MP3
Final uncertainty must be the absolute uncertainty
[4 marks]
Examiners report
A student investigates the electromotive force (emf) ε and internal resistance r of a cell.
The current I and the terminal potential difference V are measured.
For this circuit V = ε - Ir .
The table shows the data collected by the student. The uncertainties for each measurement
are shown.
The graph shows the data plotted.
The student has plotted error bars for the potential difference. Outline why no error bars are shown for the current.
Determine, using the graph, the emf of the cell including the uncertainty for this value. Give your answer to the correct number of significant figures.
Outline, without calculation, how the internal resistance can be determined from this graph.
Markscheme
ΔI is too small to be shown/seen
OR
Error bar of negligible size compared to error bar in V ✔
evidence that ε can be determined from the y-intercept of the line of best-fit or lines of min and max gradient ✔
states ε=1.59 OR 1.60 OR 1.61V«» ✔
states uncertainty in ε is 0.02 V«» OR 0.03«V» ✔
determine the gradient «of the line of best-fit» ✔
r is the negative of this gradient ✔
Examiners report
Almost all candidates realised that the uncertainty in I was too small to be shown. A common mistake was to mention that since I is the independent variable the uncertainty is negligible.
The number of candidates who realised that the V intercept was EMF was disappointing. Large numbers of candidates tried to calculate ε using points on the graph, often ending up with unrealistic values. Another common mistake was not giving values of ε and Δε to the correct number of digits - 2 decimal places on this occasion. Very few candidates drew maximum and minimum gradient lines as a way of determining Δε.
A student uses a Young’s double-slit apparatus to determine the wavelength of light emitted by a monochromatic source. A portion of the interference pattern is observed on a screen.
The distance D from the double slits to the screen is measured using a ruler with a smallest scale division of 1 mm.
The fringe separation s is measured with uncertainty ± 0.1 mm.
The slit separation d has negligible uncertainty.
The wavelength is calculated using the relationship .
When d = 0.200 mm, s = 0.9 mm and D = 280 mm, determine the percentage uncertainty in the wavelength.
Explain how the student could use this apparatus to obtain a more reliable value for λ.
Markscheme
Evidence of used ✔
«add fractional/% uncertainties»
obtains 11 % (or 0.11) OR 10 % (or 0.1) ✔
ALTERNATIVE 1:
measure the combined width for several fringes
OR
repeat measurements ✓
take the average
OR
so the «percentage» uncertainties are reduced ✓
ALTERNATIVE 2:
increase D «hence s»
OR
Decrease d ✓
so the «percentage» uncertainties are reduced ✓
Do not accept answers which suggest using different apparatus.
Examiners report
A very easy question about percentage uncertainty which most candidates got completely correct. Many candidates gave the uncertainty to 4 significant figures or more. The process used to obtain the final answer was often difficult to follow.
The most common correct answer was the readings should be repeated and an average taken. Another common answer was that D could be increased to reduce uncertainties in s. The best candidates knew that it was good practice to measure many fringe spacings and find the mean value. Quite a few candidates incorrectly stated that different apparatus should be used to give more precise results.
An experiment is conducted to determine how the fundamental frequency f of a vibrating wire varies with the tension T in the wire.
The data are shown in the graph, the uncertainty in the tension is not shown.
It is proposed that the frequency of oscillation is given by f2 = kT where k is a constant.
Draw the line of best fit for the data.
Determine the fundamental SI unit for k.
Write down a pair of quantities that, when plotted, enable the relationship f2 = kT to be verified.
Describe the key features of the graph in (b)(ii) if it is to support this relationship.
Markscheme
Any curve that passes through ALL the error bars ✔
kg–1 m–1 ✔
f2 AND T
OR
f AND
OR
log f AND log T
OR
ln f AND ln T ✔
graph would be a straight line/constant gradient/linear ✔
passing through the origin ✔
Examiners report
Most candidates correctly drew curves which passed through all the error bars, some tried to draw straight lines. Quite a few did not draw any line, leaving the question unanswered. Candidates need to make sure to check that they read the question paper carefully.
Determining the fundamental units of K (kg-1 m-1 ) was difficult for most candidates.
These questions were not well understood, but a few candidates were able to state that a plot of f2 versus T would give a straight line through the origin.
These questions were not well understood, but a few candidates were able to state that a plot of f2 versus T would give a straight line through the origin.
In an investigation a student folds paper into cylinders of the same diameter D but different heights. Beginning with the shortest cylinder they applied the same fixed load to each of the cylinders one by one. They recorded the height H of the first cylinder to collapse.
They then repeat this process with cylinders of different diameters.
The graph shows the data plotted by the student and the line of best fit.
Theory predicts that H = where c is a constant.
Suggest why the student’s data supports the theoretical prediction.
Determine c. State an appropriate unit for c.
Determine c. State an appropriate unit for c.
Identify one factor that determines the value of c.
Markscheme
theory «» predicts that H3 ∝ D2 ✔
graph «of H3 vs D2 » is a straight line through the origin/graph of proportionality ✔
Allow gives H3 = c3D2 for MP1.
Do not award MP2 for “the graph is linear” without mention of origin.
evidence of gradient calculation to give gradient = 3.0 ✔
c3 = 3.0 ⇒ c = 1.4 ✔
evidence of gradient calculation to give gradient = 3.0 ✔
c3 = 3.0 ⇒ c = 1.4 ✔
the load/the thickness of paper/the type of paper/ the number of times the paper is rolled to form a cylinder ✔
Examiners report
Load on a cylinder. The question was successful for candidates well prepared to write conclusions in their lab reports. Theory in the stem of the question predicts a directly proportional relationship between H and D2/3, which graphed are H3 and D2. Well prepared candidates were able to identify, that the theory predicts that H3 should be directly proportional to D2 and that this proportionality can be seen from the graph. Many candidates were able to mention that the relationship was linear and passed through the origin (as an alternative to proportional). However, a common response mentioned only linear or linear regression which is not sufficient to fully demonstrate proportionality.
Part b) was the most difficult part of section A, but still accessible. Many candidates only calculated the slope of the graph and did not realise that the third root of the slope is the constant c. Some students who were able to achieve the numerical value of c=1.4 struggled to establish the correct unit - perhaps lacking confidence or familiarity with the notion that a unit could be raised to a fractional index.
Part b) was the most difficult part of section A, but still accessible. Many candidates only calculated the slope of the graph and did not realise that the third root of the slope is the constant c. Some students who were able to achieve the numerical value of c=1.4 struggled to establish the correct unit - perhaps lacking confidence or familiarity with the notion that a unit could be raised to a fractional index.
In c) most of the candidates well identified the load or the type of the paper as possible controlled variables. A common mistake here was answer discussing the height or the diameter of the cylinders.